Maths
Mathematics is a tool for everyday life. Our school believes that every child is entitled to a high-quality mathematics education allowing mastery for all pupils and providing opportunities for children at greater depth.
We aim for children to have an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject.
Intent
It is our belief that our pupils should become fluent in the fundamentals of mathematics, so that they:
- have a well-developed sense of number values
- know by heart key number facts, e.g. times-tables and related division facts, number bonds – in line with the latest programmes of study
- apply knowledge of the above to work out connected facts
- reason mathematically, so that they:
- are able to follow a line of enquiry
- provide generalisations and proof of findings around their investigations
- are able to justify their thinking, e.g. as to why a particularly calculation strategy is the most efficient
- solve problems by applying their understanding of mathematics, so that they:
- encounter a variety of problems
- are able to select specific maths skills and/or operations
- persevere with a line of enquiry, breaking down increasingly complex problems into a series of smaller steps
Central to our approach are the 5 Big Ideas which underpin mastery in mathematics:
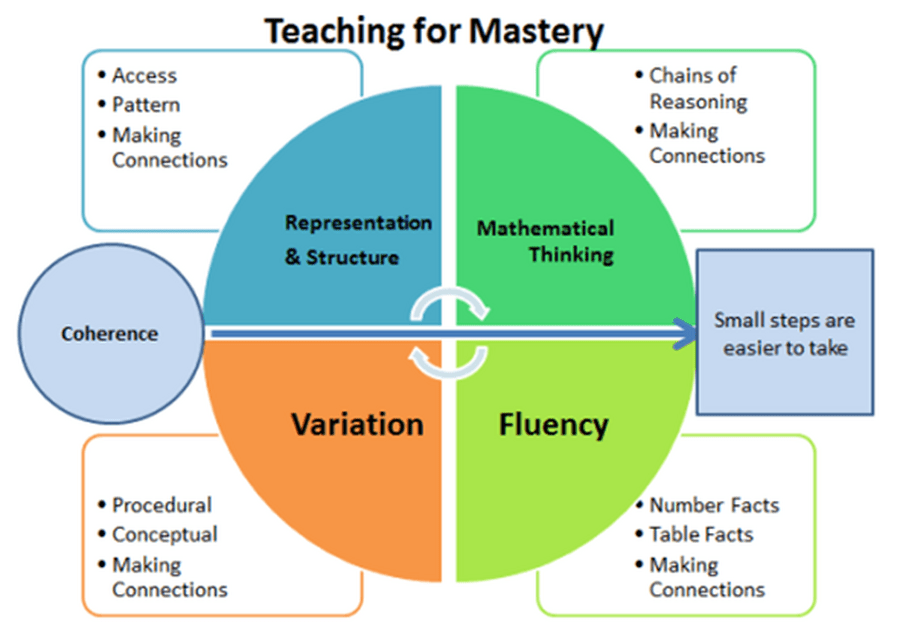
Teaching for Mastery Principles:
- Teaching is underpinned by a belief in the importance of mathematics and that the vast majority of children can succeed in learning mathematics in line with national expectations for the end of each key stage.
- The whole class is taught mathematics together, with no differentiation by acceleration to new content. The learning needs of individual pupils are addressed through careful small step scaffolding, skillful questioning and appropriate intervention is given in order to provide the necessary support and challenge.
- Factual knowledge (e.g. number bonds and timetables), procedural knowledge (e.g. formal written methods) and conceptual knowledge (e.g. place value) are taught in a fully integrated way and are all seen as important elements in the learning of mathematics.
- The reasoning behind mathematical processes is emphasised. Teacher/pupil interaction explores in detail how answers were obtained, why the method/strategy worked and what might be the most efficient method/strategy.
- Precise mathematical language in stem sentences is used by the teacher so mathematical ideas are conveyed with clarity and precision.
- Conceptual variation and procedural variation are used. These provide intelligent practice that embeds deep learning.
- Sufficient time is spent on key concepts to ensure learning is well developed and deeply embedded before moving on.
Implementation
- Children study mathematics daily following the White Rose Maths Scheme of Learning long term plan.
- NCETM PD materials are used to support planning a coherent journey using small connected steps.
- Daily maths lessons include opportunities for fluency, reasoning and problem solving.
- The vast majority of the class move through the learning at the same pace. Where needed, learning is scaffolded to support understanding of concepts.
- Children engage with a wide and varied range of concrete manipulatives, pictorial representations and abstract methodologies within each session. Cohesive use of CPA is a fundamental part of mastery in mathematics for all learners, not just those pupils with SEND. Concrete and pictorial references scaffold and strengthen understanding and are widely used as a teaching and learning tool from Foundation Stage to Year 6.
- Sessions include explicit reference to vital mathematical vocabulary and the use of stem sentences to support and encourage all children to communicate their ideas with mathematical precision and clarity. These sentence structures often express key conceptual ideas or generalities and provide a framework to embed conceptual knowledge and build understanding.
- Concrete manipulatives and pictorial representations are used to support conceptual understanding and to make links across topics.
- Careful use of questioning to support learning.
- Mastering Number is taught in EYFS and KS1 for daily fluency sessions
- In KS2 we have adopted the Clare Christie approach to teaching times tables facts.
- Children are assessed on a termly basis using NTS Mathematics.
Fluency:
In addition to our daily maths lessons, we have fluency sessions. In EYFS and KS1, we are following the Mastering Number programme which aims to equip KS1 teachers with the skills and knowledge to ensure that all children leave KS1 with strong, deep and flexible understanding of the number system.
In KS2, we have a daily times tables focus using the Claire Christie approach to learning times tables. There are 36 key facts to learn as shown in ‘Mathematics guidance: key stages 1 and 2 Non-statutory guidance for the national curriculum in England’
Our approach:
- Systematic, whole class approach to learning the times tables.
- Aims to break down the learning of the times tables into manageable chunks learning a times table at a time
- Importance of the commutative law and the relationship with division facts.
- Rote learning in which children learn the number facts AND a sound pattern
- Little and often - a two minute times table test with 40 questions in each test
We also use Times Tables Rockstars to support the children with learning their tables facts to automaticity.
Impact
- Children are happy learners who talk enthusiastically about their learning and eager to further their progress in maths
- A mathematical concept or skill has been mastered when a child can show it in multiple ways, using the mathematical language to explain their ideas, and can independently apply the concept to new problems in unfamiliar situations.
- The impact of ‘mastery’ and the emphasis on accurate use of mathematical language is evident during class/pupil discussions
- Children demonstrate quick recall of facts and procedures. This includes the recollection of the times tables.
- The flexibility and fluidity to move between different contexts and representations of mathematics.
- The ability to recognise relationships and make connections in mathematics.


















